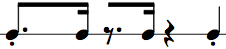 ) to demonstrate the
procedure:
) to demonstrate the
procedure:

Additionally, a "LOOP" mode is available which allows to chain programs together. It has the limitation that it can only play programs 1 - 8 in that order. You can have a program played from 0 to several times, though.
I use Eddie Harris' "Ambidextrous" riff (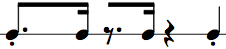 ) to demonstrate the
procedure:
) to demonstrate the
procedure:
| Rhythm | DB-88 | ||||||
|---|---|---|---|---|---|---|---|
| duration (16ths) | increment | program | beat 1 count | beat 2 count | tempo (BPM) | LOOP count | |
| 3 | lcm(3,4,5)/3 = 20 | 1 | 1 | 0 | 120 | 1 | |
| 4 | lcm(3,4,5)/4 = 15 | 2 | 1 | 0 | 90 | 1 | |
| 5 | lcm(3,4,5)/5 = 12 | 3 | 1 | 0 | 72 | 1 | |
| 4 | lcm(3,4,5)/4 = 15 | 4 | 1 | 0 | 90 | 1 | |
| n/a | n/a | 5 | irrelevant | irrelevant | irrelevant | OFF | |
| n/a | n/a | 6 | irrelevant | irrelevant | irrelevant | OFF | |
| n/a | n/a | 7 | irrelevant | irrelevant | irrelevant | OFF | |
| n/a | n/a | 8 | irrelevant | irrelevant | irrelevant | OFF | |
Instructions: Enter the timeline in the field below, e.g. "3 4 5 4" without the quotes and press Tab.
In the generated table: Change the BPM for any duration by either clicking the small arrows or click in the BPM text field and scroll up or down using the mouse wheel. Also the left ← or down ↓ arrow keys can be used to decrement the BPMs, or the up ↑ and right → arrow keys to increase. The BPMs for the other durations are adapted accordingly.
The BPMs are constrained by the increment as well as the range of BPM of the metronome, i.e. 35 - 250: If a BPM field exceeds this range, its background gets colored.Converting BPMs (musical) to seconds (physical) BPM2s : 60 / BPM = s s2BPM : 60 / s = BPM Remark: Conversion between BPM and seconds is an involution.
2, 3, 4 -> the last note is 4 sixteenths which is a quarter note, so the last note gets 120 BPM.
pd(chosen note) thus is BPM2s(120) = 60 / 120 = 1/2 s. pd(note x) = pd(chosen note) / md(note x), so pd(first note) = pd(chosen note) / md(first note) = 1/2 / 2 = 1/4 s. pd(second note) = pd(chosen note) / md(second note) = 1/2 / 3 = 1/6 s.
What would happen if we chose to assign 120 BPM to the 2nd note (md(second note) == 3)? pd(note x) = 60 / BPM(note x) // no matter what md(note x) is! pd(note y) = pd(note x) * (md(note y) / md(note x)) // simple arithmetic for physical durations BPM(note y) = 60 / [ pd(note x) * (md(note y) / md(note x)) ] BPM(note y) = 60 / [ (60 / BPM(note x)) * (md(note y) / md(note x)) ] BPM(note y) = BPM(chosen note) * md(chosen note) / md(note y).
| (3.1) BPM(note x) = BPM(chosen note) * md(chosen note) / md(note x) |
Now, convert these back to BPMs: BPM(note x) = BPM(chosen note) * md(chosen note) / md(note x) BPM(first note) = 120 * md(chosen note) / md(first note) = 120 * 4 / 2 = 240. BPM(second note) = 120 * md(chosen note) / md(second note) = 120 * 4 / 3 = 160. BPM(chosen note) = 120 * md(chosen note) / md(chosen note) = 120 * 4 / 4 = 120.
| (4.1) find a minimal integer i, that, multiplied with a given integer d, is integer divisible by integers b, c. |
The lcm task would be: Find a minimal integer i', so that it's integer divisible by a set of given integers b, c. If i' is divisible by b, c, then certainly so is i'*d. However, if d shares divisors with i', then i may be less than i', hence less than lcm(b, c). Finding the divisors of d and i' is gcd's job:
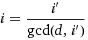
Expand the fraction with d:
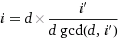
Using fact 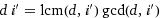 we get:
we get:
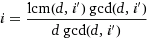
Reducing the fraction by 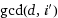 , then substituting i', finally using fact
, then substituting i', finally using fact 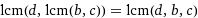 we get:
we get:
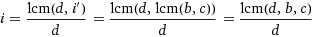
Since we made the substitution 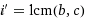 , the method applies to any number of durations {b, c, e, f, ...}, not just two {b, c} as in the proof. Thus, finally:
, the method applies to any number of durations {b, c, e, f, ...}, not just two {b, c} as in the proof. Thus, finally:
|
(4.2) The BPM we choose for a particular musical note duration d needs to be integer divisible by the increment i = lcm(all durations including d)/d. |