Rhythmic Patterns As Binary Numbers

The following text presents a concise notation for rhythmic patterns, that allows performing musical transformations on the patterns with simple arithmetic operations.

Hexadecimal notation of binary numbers

When working with rhythmic patterns, 16 binary digits (i.e. "bits") are a possible representation of a 4/4 rhythm divided into 16 16th notes. 16 bits consist of 2 bytes of 8 bits each. 8 bits can represent 2⁸ = 256 different values.

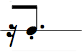
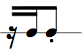
Two hexadecimal ("hex") digits (hex = to the base 16) are a common way to represent a byte value. Since the decimal ("dec") system only has 10 different ciphers, the required additional 6 digits are represented by the letters "a" to "f" (or "A" to "F").

One of the advantages of the hex system is that with a little practice, it can easily be translated to binary ("bin").

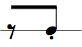
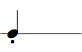
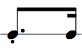
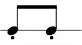
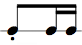
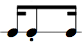
In the following table we represent the 16 possible values for 4 bits (2⁴ = 16) along with the hex, dec notation, and corresponding rhythm pattern. (4 bits, i.e. half a byte, is also called a "nibble").

The dec value of a 4-bit bin number can be calculated by multiplying the leftmost digit with 8, the next with 4, the next with 2, and the last with 1 and summing the resulting numbers together. E.g. the bin number 1101 is 1 * 8 + 1 * 4 + 0 * 2 + 1 * 1 = 13 (hex: D)

bin hex dec rhythm pattern audio

0000 0 0

0001 1 1

0010 2 2

0011 3 3

0100 4 4

0101 5 5

0110 6 6

0111 7 7

1000 8 8

1001 9 9

1010 A 10

1011 B 11

1100 C 12

1101 D 13

1110 E 14

1111 F 15

bin	hex	dec
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4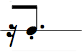
0101	5	5
0110	6	6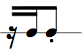
0111	7	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

The corresponding representation for 8 bits is done by concatenating two hex digits, e.g. 1011 0110 in hex notation is: 1011 (=B), 0110 (=6), thus the hex notation is B6. This can be extended to any number of digits, i.e. for a 16 bit value 4 hex digits are required, e.g. 1011 0110 0010 0101 equals B625.

Advantages

Up to this point the mapping of 16 different rhyhtmic patterns to 16 symbols may seem entirely arbitrary, if not counter-intuitive, as opposed to, e.g., a simple numbering from 1 to 16.

However, by mapping rhythmic patterns to the binary system, musical transformations on a pattern can be performed by simple arithmetic operations (as explained below).

A second advantage is the concise notation: 16 different patterns can be discerned by a single cipher. This way of referring to rhythms fosters reading music more efficiently: The reader identifies rhythm patterns as "words" as opposed to single "letters" (like the "rhythm counting" language that identifies each single of 4 16th notes with the syllables "one - e - and - a ", or the Eastman Counting System). The word-oriented learning/teaching of rhythm patterns is more in the tradition of Zoltán Kodály and Edwin Gordon. See also this article.

Shifting

Typical operations that I personally like to perform on rhythmic patterns is shifting them by a 16th note to the left or to the right in musical time.

Using the binary notation, this shifting is done by multiplying the corresponding number by 2 or by dividing it by 2.

E.g. the original pattern "6" (0110) is shifted left in musical time by multiplying it by 2, resulting in 6*2 = 12 (hex:"C", bin:"1100"). Shifting it right by 2 means dividing it by 2, resulting in 6/2 = 3 (bin: "0011").

Remark: When shifting a pattern of the form 1xxx to the left by multiplication, the first "1" would be lost. Likewise, when shifting a pattern of the form xxx1 to the right by division, the last "1" would be lost. For this reason, a circular shift operation should be used instead of just a division or multiplication.

Complementary Rhythms

Creating the complementary pattern to a given original pattern is another interesting operation, which can be done by subtracting the given original pattern number from 15.

E.g. what is the complementary pattern to the given pattern 1010? 1010 is the pattern "A" (dec: 10). 15 - 10 = 5, bin: 0101.

Exercises

My recommendation is to first learn the sixteen patterns by rote. This is best done by going on a walk with a friend and posing each other rhythmic exercises, e.g. "Sing me the pattern D3". Or one of you sings a rhythm and the other spells out the corresponding hex digits.

Next, the first person sings a rhythm and the other person sings the same rhythm shifted to the left and then to the right in musical time (by first determining the pattern identifying number and then dividing or multiplying the number and then singing the pattern identified by the resulting number). Or the other person sings the complementary rhythm (by first determining the pattern identifying number and then subtracting that number from 15 and then singing the pattern identified by the resulting number).

Examples

Riff stolen from Eddie Harris, "Ambidextrous": 9108. In this sound example, the riff is shifted backwards in musical time, resulting in the (repeated) patterns:
9108 4884 2442 1221. Here's the same riff with a bassline for easier orientation.
This example shows a bass line superimposing a 3 and a 5 pattern. The higher pitched notes are the complementary of the resulting rhythm. It merely shows a rhythm and its complementary, but since they're odd meters I can't represent them as binary yet.
This example shows the pattern 8 repeatedly divided by 2, resulting in the repeated pattern 8421.

Outlook

As mentioned in the remark, the shifting operations should be circular shifts instead of simple multiplication and division.

I'm still working on the arithmetic operation to create the reverse of a given rhythm, e.g. 1101 reversed would be 1011. Considering that it's the pairing of 16 patterns with another 16 patterns it might be worth just learning them by rote...

This principle should be extended to ternary rhythms and odd meters.

Thanks

To Swedish sax player Oskar Forsberg for his openness to work on stuff with an uncertain outcome and comments/corrections on this text.