Loop Feedback Control

Observation

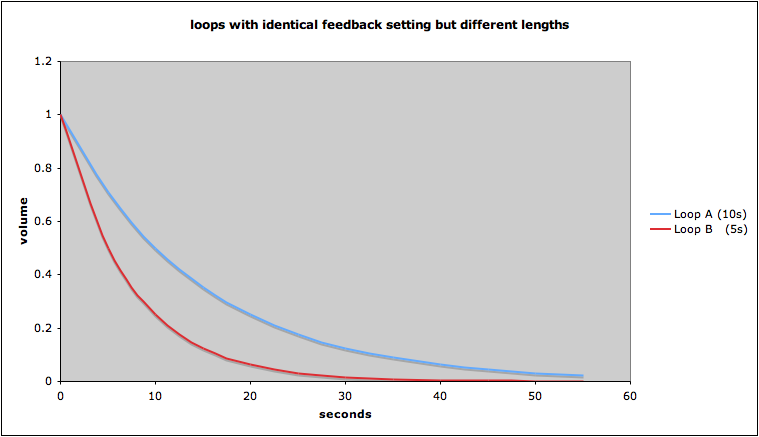
The shorter a loop the more quickly it fades out.

Explanation

The feedback control sets the amount by which the volume is reduced per loop repetition. Thus, a shorter loop's volume will decrease by the same amount within less time than a longer loop.

Example

Feedback is set to 50%.
Loop A duration 10 s, feedback will decrease by 50% per repetition, i.e. every 10 seconds.
Loop B duration 5 s, feedback will decrease by 50% per repetition, i.e. every 5 seconds.
After 10 seconds Loop A will have diminished to 50%, Loop B will have diminished to 50% * 50% -> 25%

(assuming the feedback was moved exponentially down from 100% to 50% during the first run of the loop)

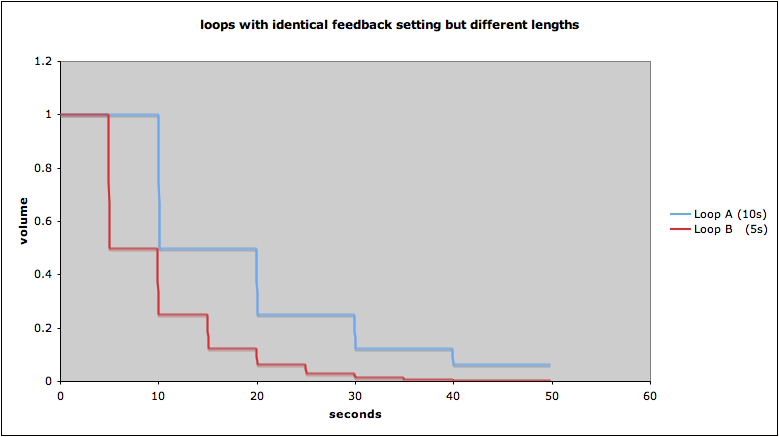
(assuming the feedback was moved briskly down from 100% to 50% during the first run of the loop. Thanks to Andy Butler for this graphic and for making the point.)

Parameters

Parameter	Symbol	Unit	Range	Domain
feedback	F	% (percent)	0-100	integer
loop duration	LD	s (seconds)	[0,...	real
process duration	PD	s (seconds)	[0,...	real
repetitions (number of)	R		[0,...	integer
volume	V	?	?	real
initial volume	V0	?	?	real

Formulas

	Formula	Description
(1)	V = V0 * (F/100)^R	Resulting volume V at the end of repetition R for a loop with a feedback setting of F
(2)	R = PD / LD	Number of repetitions depending on process duration and loop duration

Examples

What volume factor x will a 10-second-loop have decreased to after 60 seconds with a feedback setting of 80% ?

V0 * x = V0 * (F/100)^(PD/LD); (using formula (1))

x = (F/100)^(PD/LD) = 80/100^60/10 = 0.8⁶ = 0.26;

What feedback setting F will lead to a decrease in Volume by 90% within 30 seconds for a 10 second loop?

V = V0 * ( 100 - 90 ) / 100; (decrease by 90%)

V0 * 0.1 = V0 * (F/100)^(PD/LD); (using formula (1))

F = 0.1^(1/3) * 100 = 46 (59 in MIDI terms).

How many repetions R does it take until a loop's volume will have decreased to 10% with a feedback setting of 90% ?

V = V0 * 0.1;

V0 * 0.1 = V0 * (F/100)^R; (using formula (1))

0.1 = (9/10)^R;

log (0.1) = R * log (0.9);

R = log(0.1) / log (0.9) = 22;

Remarks

Changes of the feedback setting will only be audible in the next repetition of the loop.
Gestures with the feedback control will be recorded with the loop and become part of it.
We're using 100 as the maximum for the feedback setting. When using the EDP, maximum setting is 127 (due to MIDI). Thus, the formula (1) above would read: V = V0 * (F/127)^R
Volume in the text refers to Amplitude (not Loudness).

Thanks

Andy Butler for corrections.